In 2021, I wrote a brief piece, Alliterative Affinities: Do Parents Select First Names to Match Surnames? In short, the answer was yes—unless your name starts with a “J”. Unfortunately, the data for the article came from the 1930 Census. Now, I’ve updated the results with much more recent data.

I use up-to-date voter registration data from the North Carolina State Board of Elections. In this update, I’ll ditch the digression on baby names and whether names can have a causal effect on a child’s outcomes in later life.

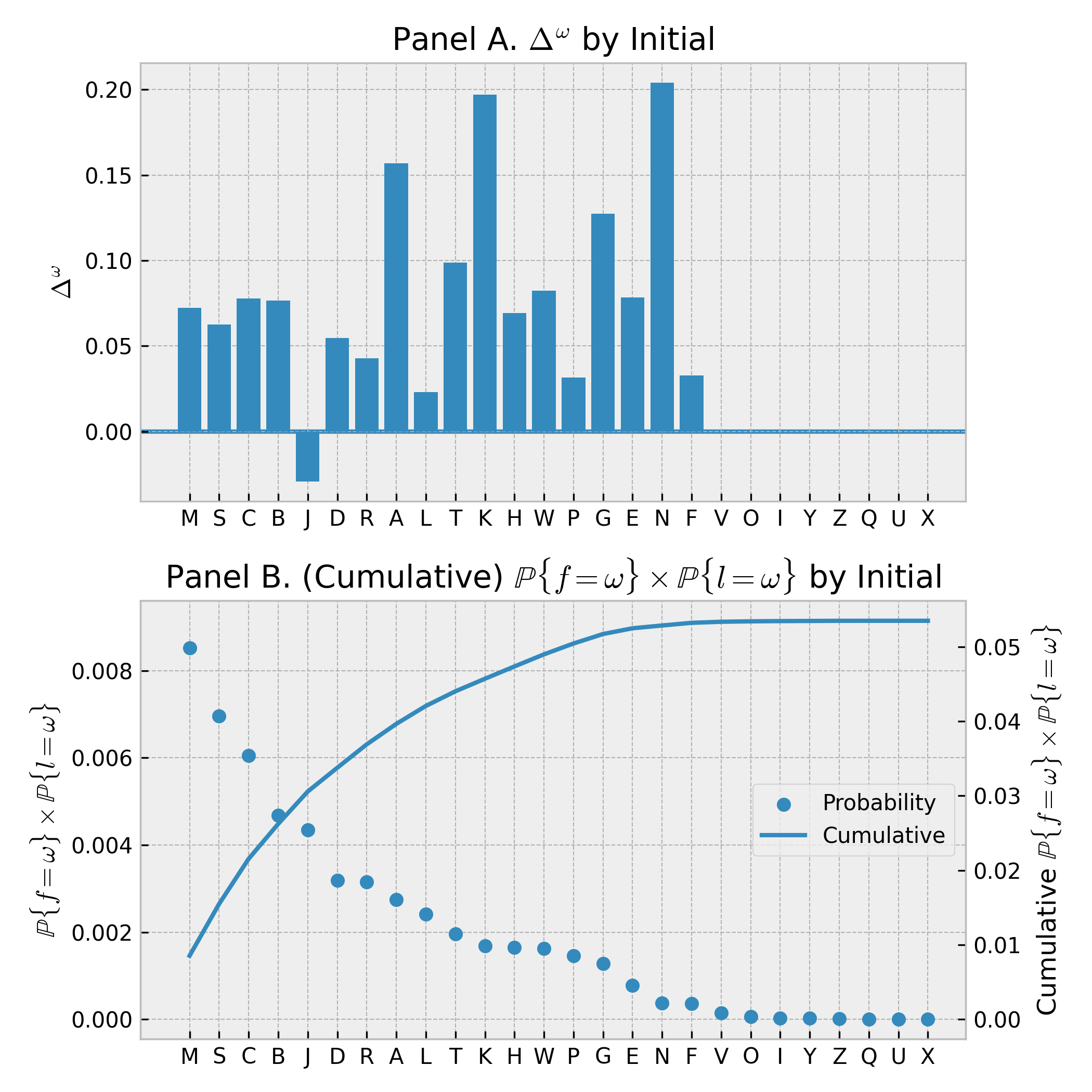
Let’s say $f$ is an individual’s first initial and $l$ is their last initial. I denote the probability that an individual’s first name starts with “A” as $\mathbb{P}\{f = A\}$, while the associated last-initial value is $\mathbb{P}\{l = A\}$. We’ll consider the probability of an alliterative pair of names beginning with “A”, $$ \mathbb{P}\{f = A \land l = A\}. $$ I then compare this value to an independent benchmark: $$ \mathbb{P}\{f = A\} \times \mathbb{P}\{l = A\}, $$ which is the probability of an alliterative pair of names beginning with “A”, if first and last initials were independent. I then calculate the percent difference between these two values $$ \Delta^{A} \equiv \frac{\mathbb{P}\{f = A \land l = A\}}{\mathbb{P}\{f = A\} \times \{l = A\}} - 1. $$

I repeat this process for all letters in the alphabet, $\omega \in \Omega$. I summarize $\Delta^{\omega}$ in Panel A of Figure 1 for the 18 most common alliterative combinations (as measured by the independent benchmark given above). For the remaining eight letters, the lower denominators result in some exceedingly large $\Delta^{\omega}$ values, all of which are positive. Indeed, $\Delta^{\omega}$ is positive for every letter except “J”; alliterative pairs of “J” are 3% less common than predicted by the independent benchmark. I found this result rather surprising, as I initially expected a positive and relatively large value for $\Delta^{J}$. As far as I can gather, others are surprised too. Why are alliterative pairs of “J” so salient?

For the top 4 letters—“M”, “S”, “C”, and “B”—alliterative pairs are over 5% more common than would be expected under independence.

I now summarize these results across the alphabet. The probability that an individual has an alliterative name is $$ \sum_{\omega \in \Omega} \mathbb{P}\{f = \omega \land l = \omega\}, $$ and the probability under independence is $$ \sum_{\omega \in \Omega} \mathbb{P}\{f = \omega\} \times \mathbb{P}\{l = \omega\}. $$

While the independent benchmark predicts an alliterative frequency of 5.35%, 5.74% of names are alliterative. Accordingly, alliteration is 7.3% more likely than would be expected if first and last initial were independent.

In the original article, I excluded married women due to the common practice of adopting a spouse’s last name. I do not observe marital status in this updated analysis. However, given the increase in age at first marriage and (I suspect) decreased tendency of taking a spouse’s last name, I expect gender to matter less compared to the 1930 data. When I restrict the sample to men, alliteration is 7.4% more likely than predicted under independence, a slight increase.